Tudo o que você precisa saber sobre notação Big O e tipos de complexidade
Um guia sobre complexidade de algoritmos e análise de eficiência.
O que você precisa saber
Software é, por natureza, movido a dados. Muitos dados. E fazer uso desses dados é o objetivo da programação. Para que um programa use esses dados, muitas vezes precisa começar ordenando tudo em uma ordem lógica – alfabética, cronológica, por tamanho, por data, etc.
Ordenação acontece o tempo todo e representa uma fatia importante de tudo o que é processado em computadores e na internet. É comum ouvir que Quick Sort é um dos algoritmos fundamentais por trás de muito do que a web faz hoje.
Ordenar dados é praticamente um subcampo inteiro em ciência da computação, com diversos algoritmos bem definidos: Quick Sort, Bubble Sort, Selection Sort, Merge Sort, Heap Sort e muitos outros. Cada um com abordagens diferentes para chegar em resultados semelhantes.
Mas qual é o melhor?
Em geral, "melhor" significa "mais rápido". É aí que entra Big O. A notação Big O, às vezes chamada de análise assintótica, analisa principalmente quantas operações um algoritmo precisa para ordenar uma coleção muito grande de dados. Isso é uma medida de eficiência e permite comparar diretamente um algoritmo com outro.
Ao construir um aplicativo pequeno, com poucos dados, esse tipo de análise muitas vezes é desnecessária. Mas quando você trabalha com volumes enormes – como redes sociais ou grandes e-commerces com muitos usuários e produtos – pequenas diferenças entre algoritmos podem se tornar muito relevantes.
Como funciona a notação Big O
Big O classifica a eficiência de um algoritmo usando "O" e "n" (por exemplo, "O(log n)"), onde:
- O O representa a ordem de crescimento da função
- n n é o tamanho da entrada (por exemplo, o comprimento do array a ser processado)
Por exemplo, se um algoritmo exige o seguinte número de operações: f(n) = 6n⁴ − 2n³ + 5
À medida que n cresce muito (tende ao infinito), o termo dominante passa a ser 6n⁴. Os outros termos, 2n³ e 5, se tornam irrelevantes. O mesmo vale para o coeficiente 6. Por isso dizemos que a função tem crescimento O(n⁴).
Tipos de complexidade
O(1)
- Tempo constanteExcelenteO algoritmo leva sempre aproximadamente o mesmo tempo, independentemente do tamanho da entrada. Isso significa que ele não depende do número de elementos processados.
Exemplos:
- Acesso direto em array
- Busca em tabela hash
- Operações push/pop em pilha
O(log n)
- Tempo logarítmicoExcelenteO tempo de execução cresce de forma logarítmica em relação ao tamanho da entrada. A cada passo, o problema é reduzido (por exemplo, pela metade).
Exemplos:
- Busca binária
- Operações em árvores balanceadas
- Busca em skip list
O(n)
- Tempo linearBomO tempo cresce proporcionalmente ao tamanho da entrada. Em geral, cada elemento é processado uma vez.
Exemplos:
- Busca linear
- Percorrer um array
- Encontrar mínimo/máximo
O(n log n)
- Tempo linearítmicoBomCombina crescimento linear com logarítmico. É típico de algoritmos eficientes de ordenação baseados em dividir e conquistar.
Exemplos:
- Merge sort
- Heap sort
- Quick sort (caso médio)
O(n²)
- Tempo quadráticoRegularO tempo cresce com o quadrado do tamanho da entrada. Costuma aparecer em loops aninhados, quando cada elemento é comparado com todos os outros.
Exemplos:
- Bubble sort
- Selection sort
- Loops duplos aninhados
O(2ⁿ)
- Tempo exponencialRuimO tempo dobra a cada novo elemento na entrada. Fica rapidamente inviável, mesmo para tamanhos moderados.
Exemplos:
- Fibonacci recursivo ingênuo
- Geração de subconjuntos
- Combinações por força bruta
O(n!)
- Tempo fatorialRuimO tempo cresce de forma fatorial à medida que o tamanho da entrada aumenta. É extremamente lento, aceitável apenas para entradas bem pequenas.
Exemplos:
- Caixeiro viajante por força bruta
- Geração de todas as permutações
- Busca exaustiva em grafos
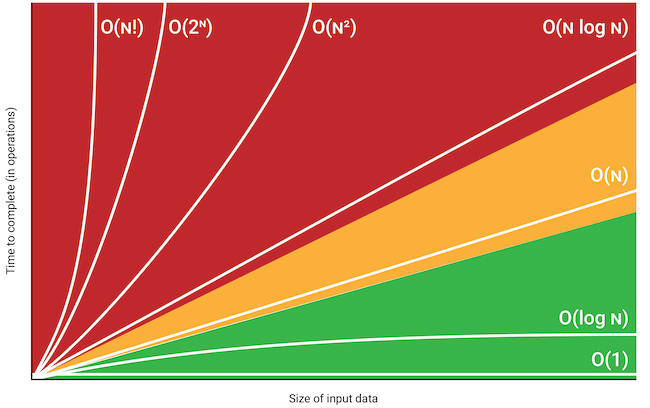
Algoritmos comuns e suas classificações
Entre os algoritmos de ordenação mais usados, O(n log n) costuma ser a melhor complexidade possível. Quick Sort, Heap Sort e Merge Sort são exemplos clássicos. Quick Sort é frequentemente o padrão em muitas bibliotecas de linguagens.
Não existe um único algoritmo mais rápido em todos os cenários. O desempenho depende muito de como os dados chegam (ordenados, quase ordenados, aleatórios, etc.). Cada algoritmo tem casos melhores e piores.
- Quick Sort: Quick Sort: Normalmente o padrão, competindo com Merge Sort e Heap Sort, também classificados como O(n log n).
- Heap Sort: Heap Sort: Também O(n log n), mas na prática costuma ser mais lento que Quick Sort in-place.
- Merge Sort: Merge Sort: É estável, ou seja, preserva a ordem relativa de elementos iguais na saída, ao contrário do Quick Sort in-place e do Heap Sort.
- Bubble / Insertion / Selection Sort: Bubble / Insertion / Selection Sort: Executam em O(n²), o que, para entradas grandes, pode ser muito mais lento do que algoritmos O(n log n).
Por que isso importa?
Se a linguagem já oferece um sort eficiente, por que se preocupar com algoritmos e Big O? E por que empresas cobram isso em entrevistas?
Porque estudar Big O ajuda a desenvolver intuição de eficiência. Ao lidar com grandes volumes, você passa a enxergar onde estão os gargalos e onde otimizar gera mais ganho. Isso também se conecta com análise de sensibilidade, importante para resolver problemas reais.
Se você está se preparando para entrevistas ou quer fortalecer sua base em ciência da computação, entender notação Big O e complexidade vai te dar vantagem e ajudar a demonstrar melhor seu potencial.
Conclusão
Entender complexidade de algoritmos não é só para passar em entrevista. É sobre escrever código mais eficiente, tomar decisões de arquitetura melhores e antecipar problemas de performance. Em muitos casos, você também precisa considerar a complexidade de espaço, escolhendo algoritmos que usam menos memória quando necessário.